CODE
#include<stdio.h>
#include<math.h>
int main(){
float a,b,c,discr,r1,r2,sqdis;
printf("Enter the Coefficient of x(square) : ");
scanf("%f",&a);
printf("Enter the Coefficient of x : ");
scanf("%f",&b);
printf("Enter the Contant Term : ");
scanf("%f",&c);
discr =(b*b)- (4*a*c);
if(a==0){
printf("Since Coefficient of x(square) is zero hence it is not a QUADRATIC EQUATION\n");
}
else{
if(discr<0){
sqdis= sqrt(-discr);
r1=(-b)/(2*a);
r2= (sqdis)/(2*a);
printf("Eqn %fx(square) + %f x + %f has complex roots = %f + i (%f), %f - i (%f)\n",a,b,c,r1,r2,r1,r2);
}
else if(discr==0){
r1=(-b)/(2*a);
printf("Eqn %fx(square) + %f x + %f has one real root = %f\n",a,b,c,r1);
}
else{
sqdis= sqrt(discr);
r1= ((-b)+ sqdis)/(2*a);
r2= ((-b)- sqdis)/(2*a);
printf("Eqn %fx(square) + %f x + %f has two distinct real roots = %f , %f \n",a,b,c,r1,r2);
}
}
return 0;
}
We first of all calculate discriminant so that we can conclude whether roots are equal, distinct or imaginary.
discr =(b*b)- (4*a*c);Now if roots are imaginary i.e. discr < 0, first we calculate square root of modulus of discriminant then we calculate real and imaginary parts of roots in r1 and r2 respectively.
sqdis= sqrt(-discr);
r1=(-b)/(2*a);
r2= (sqdis)/(2*a);Roots will be r1 + r2 i and r1 – r2 i .
Now if roots are Equal i.e. discr = 0 then Roots are calculated and stored in r1.
r1=(-b)/(2*a);Now if roots are real and distinct,first we calculate square root of modulus of discriminant then we calculate and store both roots in r1 and r2 respectively.
sqdis= sqrt(discr);
r1= ((-b)+ sqdis)/(2*a);
r2= ((-b)- sqdis)/(2*a);OUTPUT
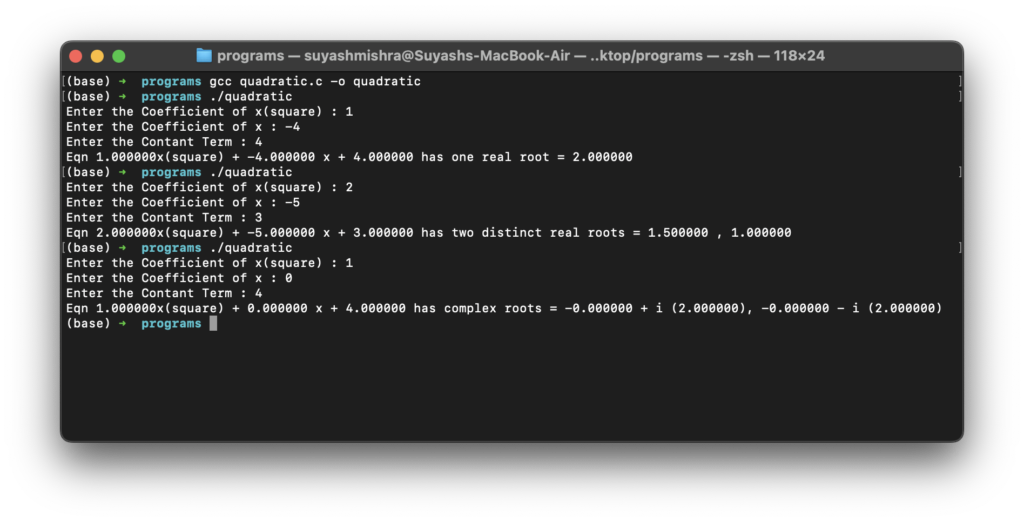



Very Informative